[地球流体電脳倶楽部]
[dcmodel |
dcmodel-tools]
[numexp]
[spmodel]
ここでは,雷雲を想定した質量強制を与えた1.5層浅水計算の実験結果を示す.
- 実験結果
- 方程式系
\begin{align}
& \frac{D \boldsymbol{u}}{D t} + g' \nabla_z h + f \boldsymbol{k} \times \boldsymbol{u} = - \boldsymbol{D}_u, \\
& \frac{D g'h}{D t} + g'h (\nabla_z \cdot \boldsymbol{u}) = \sum S_{storm} + S_{rad} - D_{g'h} . \\
\end{align}
- 強制項
質量強制項
\begin{align}
S_{storm} = s \cdot \exp \left [- \frac{R^2}{R_{storm}^2} - \frac{(t^*-t_0)}{\tau_{storm}^2} \right ]
\end{align}
\(s = 5, \alpha = 0.5\)
放射緩和項
\begin{align}
S_{rad} = - \frac{\langle g'h \rangle - g'h_{eq}}{\tau_{mass}} - \frac{g'h - \langle g'h \rangle}{\tau_{APE}}
\end{align}
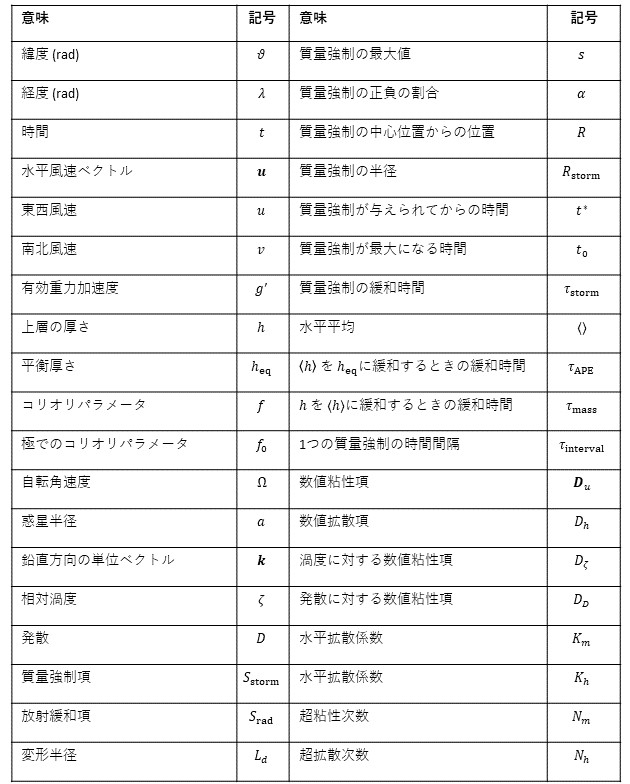
- パラメータの説明
- 実験結果
- 方程式系
Showman (2007) の連続の式に質量調整項 : \(S_{mass}\) が加わる.
\begin{align}
& \frac{D \boldsymbol{u}}{D t} + g' \nabla_z h + f \boldsymbol{k} \times \boldsymbol{u} = - \boldsymbol{D}_u, \\
& \frac{D g'h}{D t} + g'h (\nabla_z \cdot \boldsymbol{u}) = \sum S_{storm} + S_{mass} +S_{rad} - D_{g'h} . \\
\end{align}
質量調整項
\begin{align}
S_{mass} = - \left \langle \Sigma S_{storm} \right \rangle
\end{align}
-
A. P. Showman:
Numerical simulations of forced shallow-water turbulence:
Effects of moist con-vection on the large-scale circulation of jupiter and saturn
J. Atomos. Sci. 64(9):3132-3157, Sept. 2007
-
S. R. Brueshaber, K. M. Sayanagi, and T. E. Dowling:
Dynamical regimes of giant planet polar vortices
Icarus, 323:46-61, May 2019