/地球流体セミナー
/講演資料一覧
/2001-08-22/
水惑星で SST の緯度経度と全球平均を変えたら大循環はどうなるの?
大淵 済 (地球フロンティア モデル統合化領域)
2001 年 8 月 23 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.
目次

|
大循環とは何か
- ハドレー循環, 対流圏中緯度ジェット, 擾乱(波動)に注目
- これで十分か ?
本研究の動機
|

|
NJR AGCM (CCSR/NIES AGCM 5.4 の並列化版) T42L20
- 積雲パラメタリゼーションは Arakawa-Schubert
- 放射スキームは中島映至モデル (CCSR/NIES AGCM)
- 緯度方向に 64 点, 経度方向には 128 点,
スペクトル空間ではそのうちの 1/3 の情報を捨てている(エリアシング対策)
- 最下層(フラックス面)は σ=0.990 (z=70 m), 最上端は σ=0.01 (z=30 km).
実験設定
- 地表は全て海面, その温度分布は南北対称な固定分布を与える.
- 日射は陽に与えない.
地表面からの圏熱, 潜熱, 赤外放射で循環が駆動される.
- オゾンなし
- CO2 は現在の濃度
- パラメータ実験数は 9;
SST の全球平均 T0 と赤道と極との間の SST の差 ΔT を変化させる.
- 計算モデル時間は各 SST 分布につき 2520 日 (7 年).
後半 1800 日 (5 年)を解析
おまけ
- データ出力間隔は 1 日
- SX5 をほとんど占有して計算
- 鉛直層数を 20 とするのは対流圏界面付近の構造をきちんと表現したいため
- オゾン層がないのでハドレー循環の到達領域を定義するのが困難だった.
本研究では質量流線関数の値から適当に決めた.
|
|
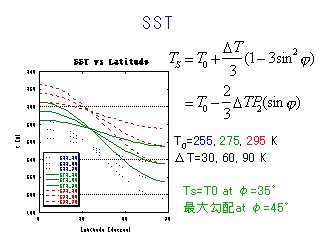
SST 分布
全球平均値と ΔT の大きさをそれぞれ 3 種類, 合計 3x3 = 9 種類.
- 最近 Hoskins らは「水惑星標準実験」なるものを提唱している.
(Neals and Hoskins, 2001).
そこでの温度分布は直線的で本研究とは異なる. Hoskins らの主な
目的はモデル比較実験, とくに積雲パラメタリゼーションのチェッ
クのためらしい (Held and Suarez (1994)
は乾燥大気だった).
- T0 = 255 実験では表面は仮想的な「凍らない水」に覆われているとしている.
表面が氷の場合は圏熱, 潜熱のフラックスが水の場合と大きく異な
る可能性がある.
- ハドレー循環の強度は赤道付近の SST 緯度勾配に敏感,
結果を解釈する際に注意が必要 (佐藤正樹氏談).
|
|
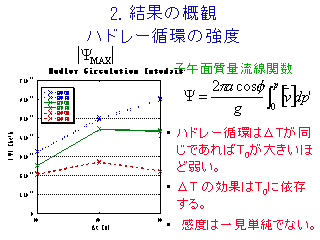
ハドレー循環の強度
- T0, ΔT に対するハドレー循環強度(質量流線関数の大きさ)の感度は
単純ではない.
- 質量流線関数には流れが強くなった効果と子午面循環の領域が広がった効果
が表れる.
|
|
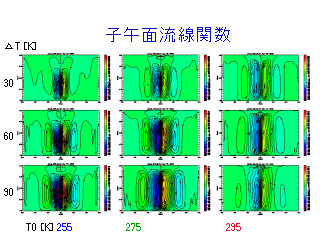
ハドレー循環の様子
- ハドレー循環の高さと幅は
- T0 , ΔT に比例して大きくなる.
- 熱帯の SST が同じ場合, だいたい同じ大きさ.
|
|
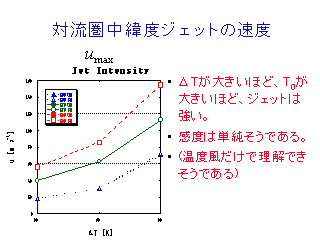
対流圏中緯度ジェットの速度
- 温度風の関係と T0 に対する圏界面高度の感度から理解できそうである.
- 地表気温の ΔT が SST の ΔT の比例しているか?
|
|
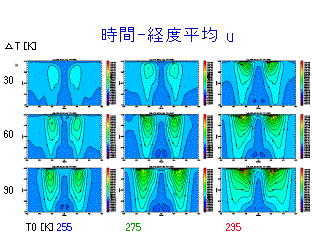
ジェットの様子
|
|
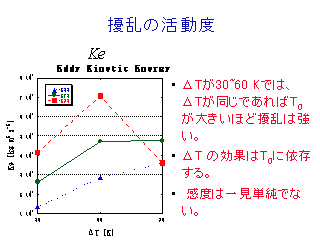
擾乱の活動度 (帯状平均からのずれ成分の運動エネルギーの全球積分値)
|
|
擾乱の活動度の様子
- T0=295 K 実験ではピークが 2 つ現れる.
不自然であるが原因はよくわからない.
|

|
まとめと問題提起
|
|
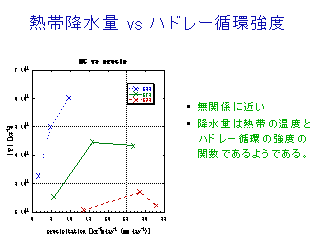
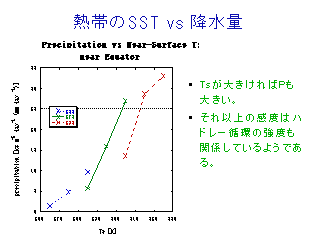
熱帯降水量 vs ハドレー循環強度
|
|
熱帯の SST vs 降水量
- Ts に比例して降水量は増える.
- ハドレー循環の強度にも依存する.
|
|
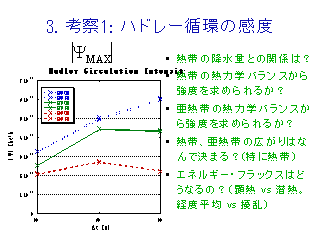
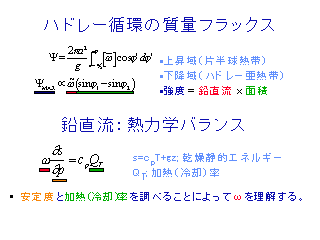
ハドレー循環の質量フラックスと熱力学バランス
|

|
熱帯での熱力学バランスの詳細
- 加熱/冷却項 Q の実体は熱帯では潜熱解放, 亜熱帯では放射冷却.
- 降水量 P が水蒸気収束によって決まると考えると鉛直流を決められない.
- ハドレー循環の強度を調べるには亜熱帯での熱力学バランスを
考えなくてはならない.
|
|
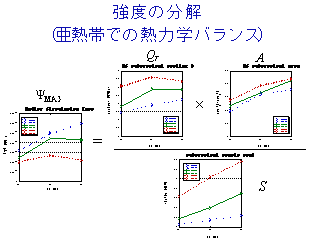
子午面循環の強度を決める要素
- Ψmax: 流線関数(水平時間平均)の最大値
- Qt : 亜熱帯(下降域)での正味の加熱率
- A : 亜熱帯(下降域)の面積
- S : 安定度(乾燥静的エネルギーの鉛直勾配)
の亜熱帯(下降域)での平均値
各実験での循環強度の解釈
- それぞれの T0 について ΔT を増加させると S, A は増加する.
S と A の Ψ に対する寄与は逆 (Ψ∝A/S) なので,
両者の効果はキャンセルする.
- Ψmax の ΔT 依存性は Qt の ΔT 依存性で説明されるようだ.
|
|
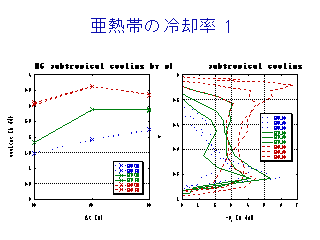
Qt (正味の加熱率)はどう決まるか?
- 放射冷却する特徴的温度は, 水蒸気の光学的厚さ(τ)が 1 程度となる高
度での温度
|
|
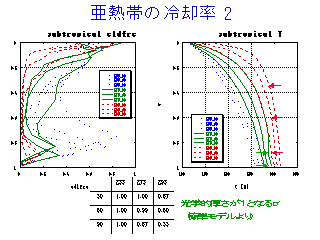
Qt (正味の加熱率)はどう決まるか?
灰色大気放射モデルに本研究の計算結果から得られる水蒸気分布を与えて計算
される τ=1 の高度は,
- T0=255 K 実験 [青] では ΔT によらず 地表
- T0=275 K 実験 [緑] では ΔT を増加させると若干地表から離れる.
- T0=295 K 実験 [赤] では ΔT を増加させると大きく変化する.
Qt が ΔT に依存しなくなる場合, τ=1 での温度が ΔT によらずほぼ一定となる.
- T0=295 K 実験
- T0=275 K 実験の ΔT=60, 90 K の場合
|
|
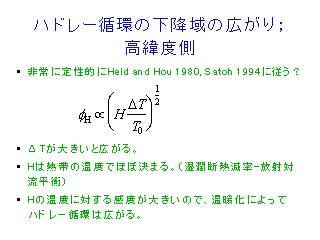
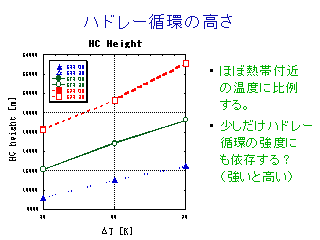
ハドレー循環の高さ
|
|
左側がモデル計算, 右側が解析的な見積もり.
傾向はだいたいあっているようにみえる.
|
|
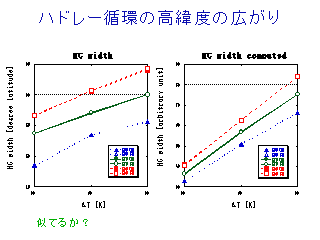
ハドレー循環上昇域の幅
- 縦軸は質量流線関数の最大値が位置する緯度.
これより低緯度側を上昇域とする.
|
|
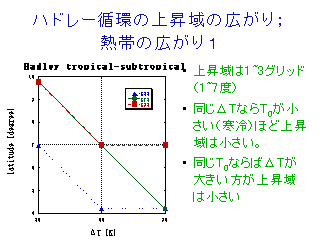
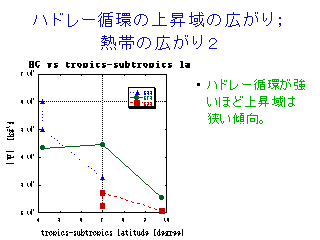
ハドレー循環上昇域の幅
- 循環強度は下降域の幅に比例.
よって循環が強いほど上昇域は狭くなる, という表現が正しい?
|
|
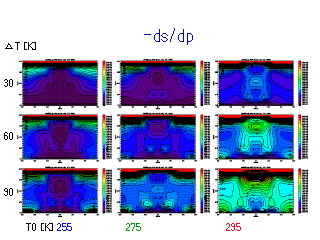
静的安定度
|
|
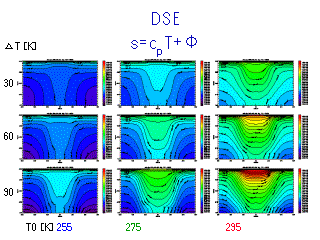
静的乾燥エネルギー (CpT + gz)
- 低緯度(熱帯+亜熱帯)では等圧面に沿って水平にほぼ一様.
- ハドレー循環の水平流によるものと想像される.
|
|
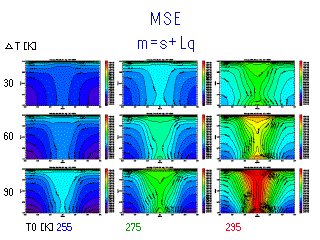
静的湿潤エネルギー (CpT + gz + Lq)
- 熱帯では鉛直にほぼ一様.
- ハドレー循環の上昇流によるものと想像される.
|
|
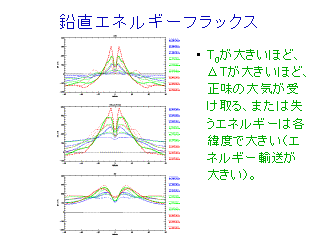
鉛直エネルギーフラックス
- 上段: 大気の正味の加熱量
- 中断: 地面から大気へ輸送される正味の熱 (顕熱 + 潜熱 + 放射)
- 下段: OLR
地面から大気への熱輸送の亜熱帯ピークは, ハドレー循環のリターンフローに
ともなう潜熱・顕熱輸送が大きいことを反映している.
OLR が熱帯で小さく, 亜熱帯で大きいのは, 熱帯の OLR は背の高い雲からの
放射, 亜熱帯では地面からの放射を見ているため. ただし観測よりもコントラ
ストが強調されている ( Peixort and Oort, 1991,
図6.14)
|
|
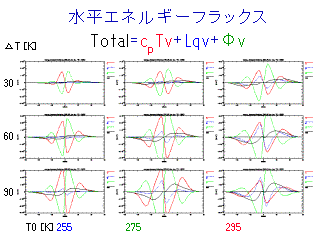
水平エネルギーフラックス (成分ごとに分離)
- T0 が大きくなると潜熱の寄与が大きくなる, とくに T0=295 K 実験で顕著.
|
|
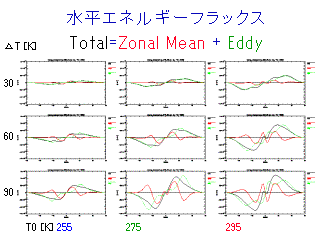
水平エネルギーフラックス (平均循環と擾乱による分離)
|
|
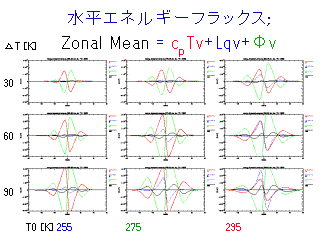
水平エネルギーフラックス (平均循環によるもの)
|
|
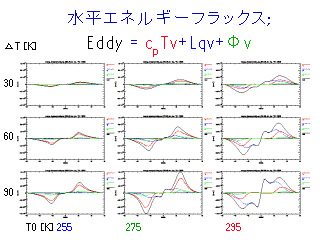
水平エネルギーフラックス (擾乱によるもの)
- T0, ΔT に比例して擾乱による輸送が大きくなる.
|

|
ハドレー循環に関する感度のまとめ
|
|
T0 が大きいほど, ΔT が大きいほどジェットは強い.
|

|
ジェットの様子
- T0 および ΔT 依存性がよく判別できる.
- 亜熱帯ジェットと中緯度ジェットの区別はあまりはっきりしない.
|
|
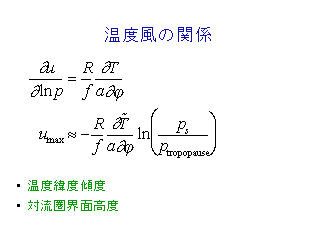
温度風の関係
|
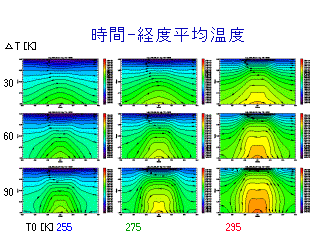
温度の時間経度平均分布
|
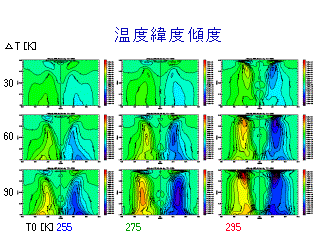
左図から求めた等圧面に沿った dT/dy
|
|
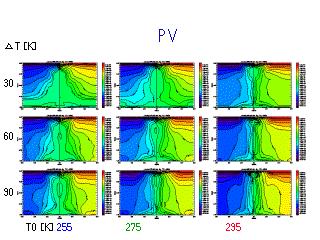
ポテンシャル渦度の子午面分布
- 2 PVU を圏界面とすると T0 が増加すると中緯度の圏界面は下ってしまう.
T0 が増加すると圏界面高度は上昇するだろう, という偏見と矛盾する.
PV がよく混ざる領域と混ざらない領域で対流圏と成層圏とを区別した方がわ
かりやすいのでは?
|
|
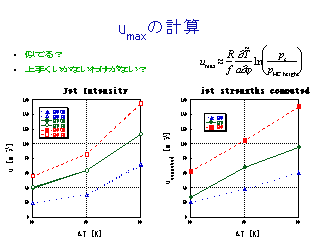
Umax の計算
- 圏界面高度をハドレー循環の厚さとする
- 左が計算値, 右か温度風の関係式からの見積もり
- 計算結果と解析的見積もりはよく一致している.
|

|
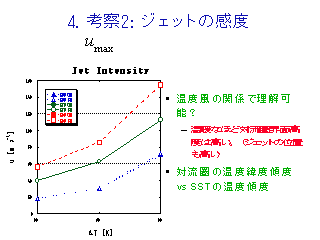
ジェットの感度のまとめ
- 温度風の関係で説明できるのはなぜ ?
- SST の南北経度から予想されるジェットの強さはどうなるか?
|
|

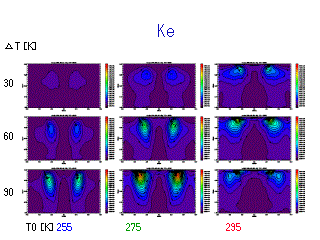
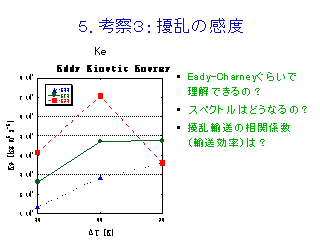
単位質量あたりの擾乱成分の運動エネルギーの時間経度平均図
|
|
水蒸気 (ポテンシャル渦度ではありません)
|
|
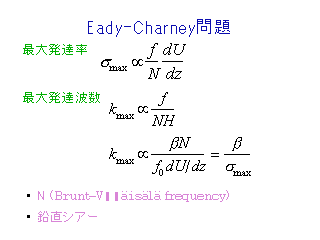
Eady & Charney モデル
- 最大発達波数の表現は Eady モデルと Charney モデルで異なる.
- T0, ΔT を大きくすると,
- Eady モデルでは最大発達波数は低波数側へ
- Charney モデルでは ?
|
|
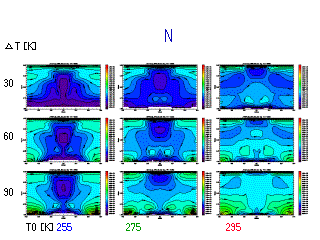
安定度
- T0 が大きいほど, ΔT が大きいほど N は大きい.
|
|
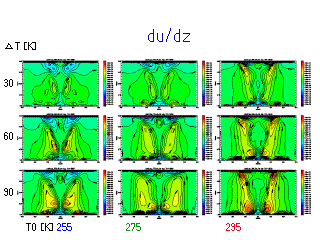
鉛直シアー
|
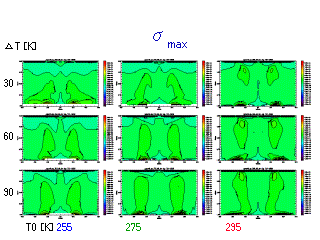
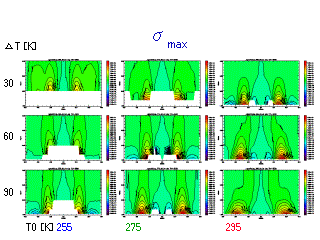
最大成長率分布
線形論の成長率の分布は意味のある情報か?
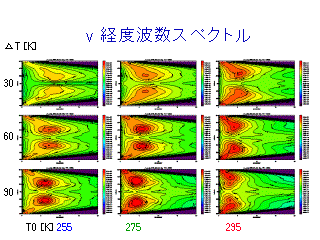
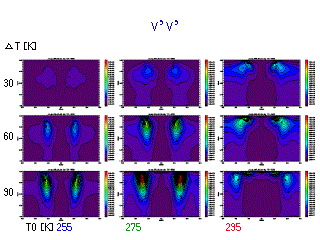
v の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
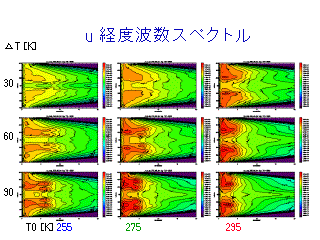
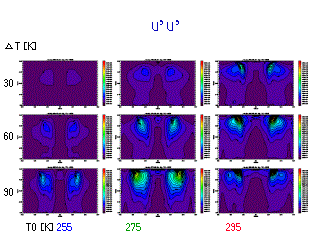
u の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
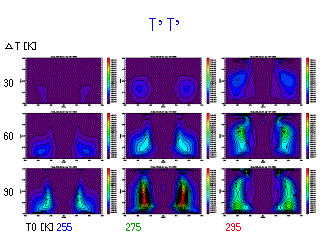
- Eady モデルから予想される k_max の T0 依存性が現れている.
- T0 が大きくなるとスペクトルのピークは低波数側へ移動.
- この特徴は以下の一連のスペクトル図において系統的に見られる.
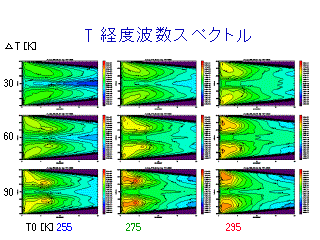
T の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
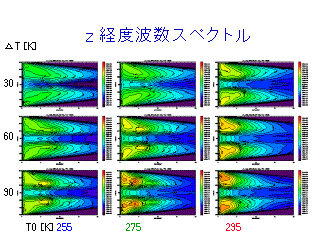
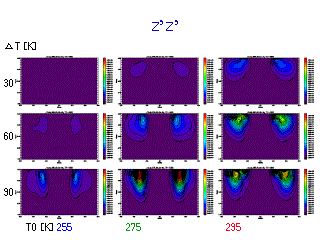
z の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
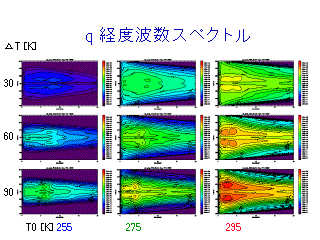
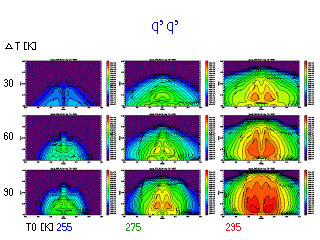
q の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
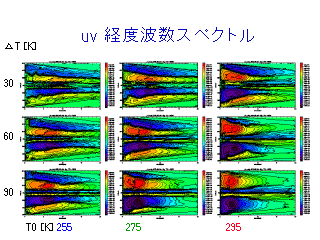
uv の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
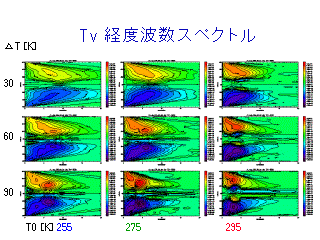
Tv の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
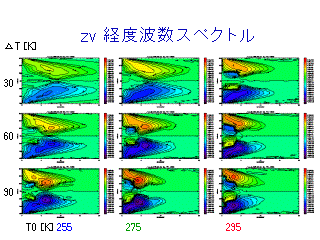
zv の東西波数スペクトル
(各等圧面でのスペクトルの鉛直積分)
|
低緯度に低波数の赤道向き輸送成分が存在する
- 擾乱による水平エネルギーフラックスの図に見られる低緯度赤道向
きの CpT と gz の輸送に対応?
- 実体はよくわからない.
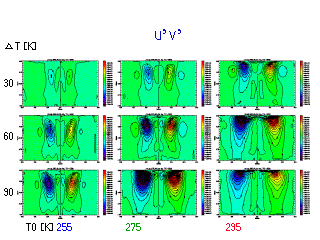
|
uv の子午面分布
|
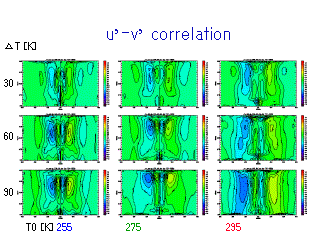
u, v の相関係数
|
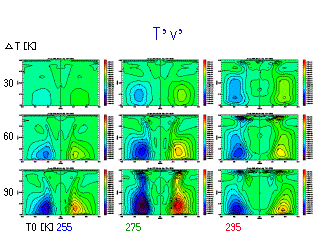
T, v の相関係数
|
- 定義は r = ab/(√a^2*√b^2)
- T0, ΔT が大きくなるにつれて相関係数は大きくなる.
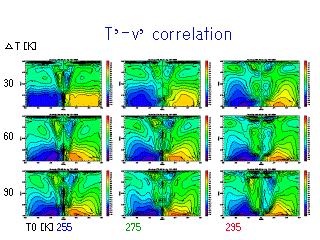
T, v の相関係数
|
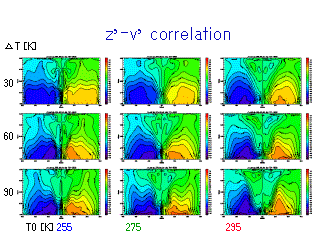
z, v の相関係数
|

|
まとめ
|

|
理論的に行うべきことはまだまだありそうだ
|
- Held, I. M., and Hou, 1980:
- Held, I. M., and M. J. Suarez, 1994: A proposal
for the intercomparison of the dynamical cores of atmospheric
general circulation models, Bull. Am. Met. Soc.,
75, 1825-1830.
-
Neale, R. B., and B. J. Hoskins, 2001a:
A standard test for AGCMs including their physical parameterizations:
I: The proposal, Atmospheric Science Letters , 1,
-
Neale, R. B., and B. J. Hoskins, 2001b:
A standard test for AGCMs including their physical parameterizations:
II: Results for the Met Office Model,
Atmospheric Science Letters , 1,
-
Peixoto, J. P., and A. H. Oort, 1991:
Physics of Climate, Springer-Verlag, New York, 520pp.
-
Satoh, M., 1994:
Odaka Masatsugu
2001-08-23
|