The turbulent diffusion coefficient is evaluated by the formula of
Klemp and Wilhelmson (1978), where
the turbulent diffusion is proportional to square root of turbulent
kinetic energy ![]() .
The value of turbulent diffusion coefficient for heat is equal
to that for momentum.
The diagnostic equation of turbulent kinetic energy is as follows.
.
The value of turbulent diffusion coefficient for heat is equal
to that for momentum.
The diagnostic equation of turbulent kinetic energy is as follows.
![]() .
.
![]() and
and ![]() are generation terms of the turbulent kinetic
energy associated with buoyancy force and wind shear, respectively.
are generation terms of the turbulent kinetic
energy associated with buoyancy force and wind shear, respectively.
The last term in left hand side of (10)
represents the dissipation rate of turbulent kinetic energy.
By using this term, ![]() in equation (5)
is given as follows.
in equation (5)
is given as follows.
The surface momentum and heat fluxes are given by the bulk
formulae, where the bulk coefficients depend on static stability
and vertical wind shear (Louis, 1979).
The bulk coefficient for heat transport has same value of that for
momentum.
![]() are the horizontal wind and temperature
at the lowest level of the model atmosphere
are the horizontal wind and temperature
at the lowest level of the model atmosphere ![]() .
.
![]() is the surface temperature.
The bulk coefficient
is the surface temperature.
The bulk coefficient ![]() is calculated as follows.
is calculated as follows.
where,
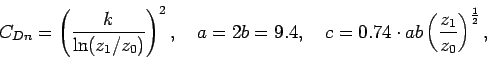 |
(18) |
and ![]() is the Karman constant (= 0.35),
is the Karman constant (= 0.35), ![]() is the roughness length.
is the roughness length.
![]() is the bulk Richardson number, which is
given as follow.
is the bulk Richardson number, which is
given as follow.
where
![]() and
are the potential temperature and that of
horizontal mean value at the lowest level of model atmosphere.
and
are the potential temperature and that of
horizontal mean value at the lowest level of model atmosphere.
| Parameters | Standard values | Note |
| 0.35 | ||
| 1 cm | Sutton et al., (1978) |