/地球流体セミナー
/講演資料一覧
/2004-03-23/
成層回転乱流の数値計算と大気スペクトル:
成層乱流におけるエネルギーカスケードに関する数値的研究とそのメソスケール大気への適用
松田 佳久(学芸大・地学)
2004 年 3 月 23 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
2 次元乱流と 3 次元乱流
3 次元乱流
2 次元乱流
問題点は....
- -5/3 乗則が出てきたら, どちらと判断すればいいのか?
- 成層効果があれば 2 次元的と思って良いのか
|

|
タイトルページ
|

|
はじめに
|
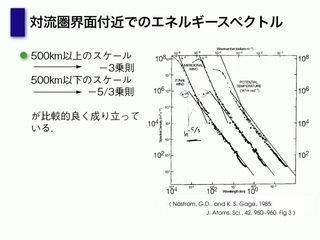
|
観測の絵
|
|
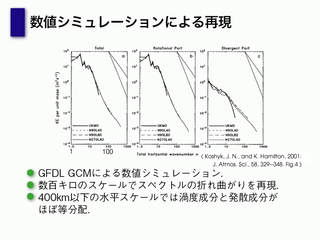
数値シミュレーションによる再現
- ちょっと見てもわかりにくいけど, 折れ曲がりを再現している
|
|
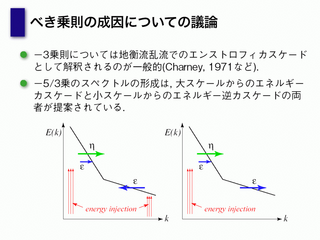
巾乗則の成因に関する議論
- 高波数をどう判断するかが大問題
- 2 つの解釈ができる
|

|
力学モデルを用いた数値実験による検証
- 安定成層の効果で 2 次元乱流的にならないか
- 現状では逆カスケードで -5/3 乗則がでたということはない
|
|
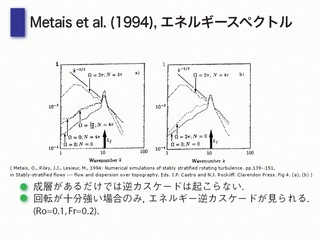
Metais et al (1994)
- 気象の状況とは全く異なる
- 成層と(ものすごく強い)回転がなければ, 逆カスケードが見られる
|

|
研究の目的
- GCM を使うと -5/3 乗則が出て来る
--> しかし何が原因で何が結果かわからない
- 現実的な GCM を用いると, いろいろなスケールでエネルギー注入が起こっているので原因と結果を切り出すことが困難
- 簡単なモデルを用いる
--> 力学的プロセスを抽出
- 乱流のパラメタリゼーションの改善
|

|
モデルの方程式
|
|
数値計算の方法
|
|
強制の与え方
- 2 つの仮説に対応する強制
- Type1: upward cascade を念頭
- Type2: downward cascade を念頭
|

|
散逸項について
- LES に基づいて渦粘性係数を決定する
- 格子点から表現できる物理量でサブグリッドスケールの運動を表現
- 成層の効果を考慮
- 水平方向にも鉛直方向にも同じように成層の効果考慮する
- 水平方向には成層の効果は入れないほうがよいのでは?
- 渦粘性に F(Ri) を加えたことが特徴. 成層の効果を取り込む
- 水平には F(Ri) を入れない方が良い?
|
|
エネルギースペクトル(type 1)
- L=20 km スケールにエネルギー注入,
- 成層を変化させて計算(横方向)
- 回転速度を変化させて計算(縦方向)
- 左上図のピークの位置がエネルギー注入スケール
- 実際の地球の条件では(ブラントバイサラ 10 分, f = 2 Ω),
-5/3 乗のアップワードカスケードは起こりにくい
- 地球の 10 倍の自転速度だと, -5/3 乗に近づく. 回転の方が重要そうだ.
結論としては, type1 の強制では -5/3 乗則を満たすのは難しい.
但し, 回転を早くすればなんとかなる
|
|
領域平均した Rossby 数と Froude 数
地球の自転パラメータではロスビー数はあまり小さくない
自転速度を 10 倍にすると, 成層によらずロスビー数は小さい
- -5/3 乗スペクトルを出すには成層よりも回転が重要
type1 では -5/3 乗則を満たすのは難しい.
|
|
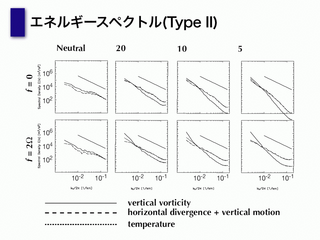
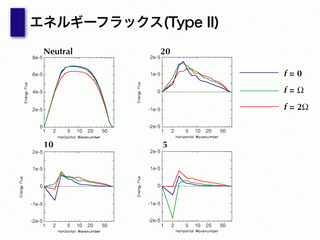
エネルギースペクトル(Type2)
- L=400 km にエネルギー注入
- どの図も -5/3 乗則を満足しているように見える
大きいスケールのところにエネルギーを注入するのが良いようだ
|
|
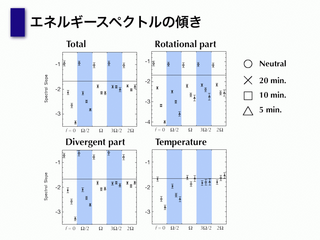
エネルギースペクトルの傾き
- 観測だと緯度によって変化しない
--> Ωを変化させて計算
|

|
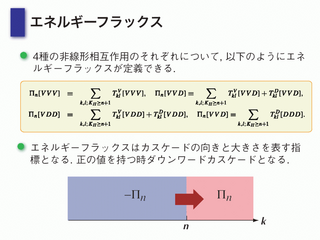
エネルギー方程式
- 鉛直方向に積分したものを取り扱う
- 3 次の非線形項が表れる
- 非線形項として, 渦モードと発散モードに分解
--> VVV: triad interaction (3 つの渦が相互作用して運動量を変化)
|
|
エネルギーフラックス
|
|
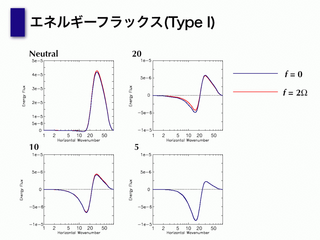
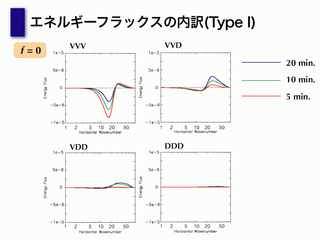
エネルギーフラックス(type1)
- マイナスの向きは upward
- マイナスが少なくて -5/3 乗則まで近付かない
- Neutral ではほぼ downward
|
|
エネルギーフラックスの内訳(Type I)
|
|
エネルギーフラックス (Type2)
|
|
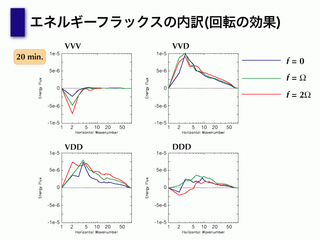
回転の効果
- VVV はアップワード
- VVV 以外はダウンワード傾向
|
|
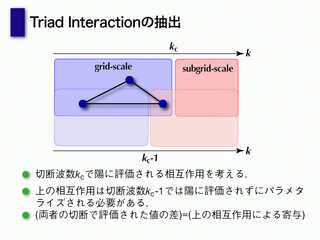
triad interaction の抽出
- サブグリッドとグリッドスケールにまたがる場合を評価
- パラメタライズの必要がある
-
|
|
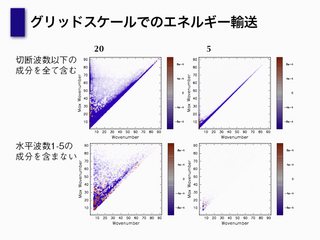
グリッドスケールのエネルギー輸送
- 縦軸: Max wave number
グリッドの切断波数みたいなもの
- 横軸: 波数
- プロットされたものはエネルギーフラックス(max wave number に来る)
- 色が濃い部分が輸送量が多い部分
- 三角形のうち, 2 辺の長さがだいたい等しくて, 他が短い triad interaction が重要
|
|
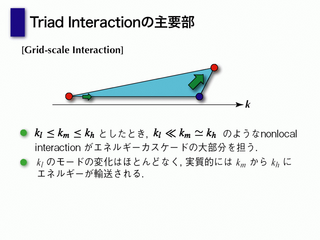
triad interaction の主要部
- 非常に近い波数間でエネルギーがカスケード
- その意味でローカルなカスケードが主要な輸送
- これまでの慣性小領域び議論と整合的
|
|
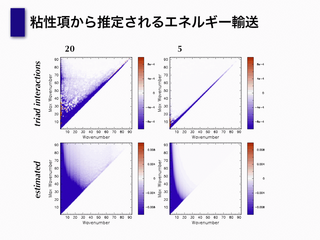
粘性項から推定されるエネルギー輸送
- explicit な世界から消えたエネルギー: サブグリッドへ
-
|
|
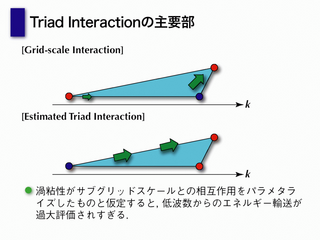
triad interaction の主要部
- 粘性項
- LES では, 定性的に誤った結果になっているように見える
|
|
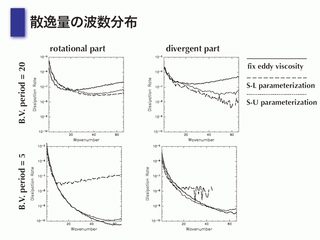
散逸量の波数分布
- 散逸に寄与する波数を, パラメタリゼーション毎に見る
- 波数が小さい方が散逸しやすい
--> 波数が小さい方がエネルギーを多く持っている.
- S-L は高波数で破綻
|
|
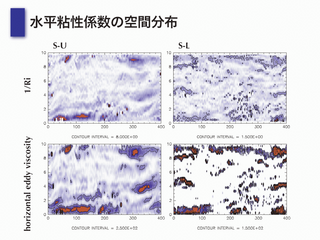
水平粘性係数の空間分布
- 空間的に一様でない
- パラメタリゼーションによって空間分布が変化
|
|
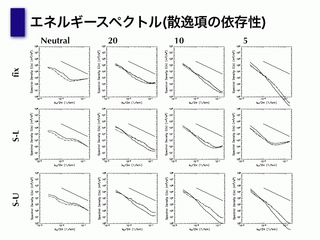
エネルギースペクトル
|

|
まとめ (1)
|

|
まとめ (2)
|

|
まとめ (3)
|
|
今後の課題
|
|
|
参考文献
- Charney, J.G., 1971:
Geostrophic turbulence, J. Atmos. Sci., 28, 1087--1095.
- Koshyk, J.N., Hamilton, K., Mahlman, J.D., 1999:
Simulation of the k/sup -5/3/ mesoscale spectral regime in the GFDL SKYHI general circulation model,
Geophysical Research Letters, 26, 843-846
- Koshyk, J. N., K. Hamilton, 2001:
The Horizontal Kinetic Energy Spectrum and Spectral Budget Simulated by
a High-Resolution Troposphere-Stratosphere-Mesosphere GCM,
JAS, 58, 329--348
- Metais, O., Riley, J.J., Lesieur, M., 1994:
Numerical simulations of stably stratified rotating turbulence. pp.139--151,
in Stably-stratified flows --- flow and dispersion over topography.
Eds. I.P. Castro and N.J. Rockiiff. Clarendon Press.
- Nastrom, G.D., Gage, K.S., 1985:
A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft,
Journal of the Atmospheric Sciences, 42, 950--960
- Ueda, H., Mitsumoto, S., Komori, S., 1981:
Buoyancy effects on the turbulent transport processes in the lower atmosphere,
Quarterly Journal of the Royal Meteorological Society, 107, 561--578
|
SUGIYAMA Ko-ichiro & ODAKA Masatsugu
2004-03-23
|


































