/地球流体セミナー
/講演資料一覧
/2003-03-17/
石岡 圭一(東大・数理科学)
2003 年 3 月 18 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|
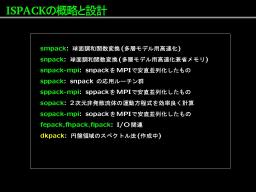
1. ISPACK の概略と設計

|
ISPACK パッケージリスト 1
|
|
ISPACK パッケージリスト 2
|

|
ISPACK の設計思想
- 性能重視, コードの可読性よりもマニュアルを充実を優先
|
2. 球面スペクトル法の概要

|
球面調和関数展開 1
|

|
球面調和関数展開 2
|

|
展開係数に対する常微分方程式の決定
|

|
具体例: 球面上の 2 次元非発散オイラー方程式 1
|

|
具体例: 球面上の 2 次元非発散オイラー方程式 2
|

|
変換法
|

|
変換の手順
|

|
球面スペクトル法のよいところ
|
3. 球面調和関数変換のベクトル化

|
ルジャンドル陪関数変換
|

|
ルジャンドル陪関数変換に必要な計算量
|

|
変換のベクトル化
- 自然な最内側 DO LOOP 変数は j (緯度方法の格子点)
|

|
最内側 DO LOOP 変数を j としたときの問題点と解決策
- ベクトル長が稼げない
- 正変換の計算が内積型 (A = A + B*C のくりかえし) となるため, 計算速度が低下する
- 最内側 DO LOOP 変数を m (経度方向の波数) とする
|

|
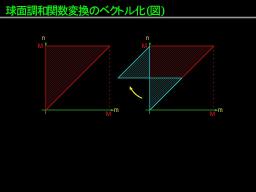
配列の並び変え
- ベクトル長を均等にするため, 展開係数を格納する配列を並び変える
|
|
三角形切断の場合
|
4. 球面調和関数変換の省メモリ化

|
ルジャンドル陪関数の格納に必要なメモリ
|

|
省メモリ化の骨子:
|

|
省メモリ化の手順 1
|

|
省メモリ化の手順 2
|

|
省メモリ化の手順 3
|
5. 球面調和関数変換の回数の削減

|
平面上の 2 次元非発散流体の場合
|

|
球面上の 2 次元非発散流体の場合 1
|

|
球面上の 2 次元非発散流体の場合 2
- 上手に式を変形してから考えると 4 回の変換で済む
|

|
球面上の浅水流体の場合 1
|

|
球面上の浅水流体の場合 2
|
6. 時間積分法に関する工夫

|
浅水系の問題
|

|
時間積分法に関する工夫 1
- 球面調和関数によるスペクトル法は展開関数が重力波の固有モードに対応しているので, 差分法に比べ高精度の計算を安定に行うことができる
- 問題を一般化する
|

|
時間積分法に関する工夫 2
- 球面調和関数によるスペクトル法は展開関数が重力波の固有モードに対応しているので, 差分法に比べ高精度の計算を安定に行うことができる
- 問題を一般化する
|

|
時間積分法に関する工夫 3
|

|
具体例: 4 次のルンゲ-クッタ法を用いた場合
|
参考文献
Odaka Masatsugu
2003-03-20
|

































