概要
2次元平面内に並行に置かれた壁の間を一方向に流れる流体の運動を考える. 流体の速度分布は平面ポアズイユ流(plane Poiseuille flow)で, $x$ 方向には一様であるとする.このときの流れの安定性を数値的に調べる.
背景
並行に置かれた壁に挟まれた流体が一方向に流れるとき、 レイノルズ数(Reynolds number)が低い(例えば数千以下の)ときには 平面ポアズイユ流のような速度分布になり,その流れは2次元的である. 流れのレイノルズ数を上げていくと,最初に2次元的な不安定が起こり, さらにレイノルズ数を上げると3次元的な不安定が起こる. 従って,低レイノルズ数では2次元系で安定性を考えれば十分である. これは,例えば矩形の管路内での安定性を調べることに相当する.
平面ポアズイユ流とは,管路内の流体の $x$ 方向の速度分布が $1 - y^2$ のように $y$ に依存する流れのことを言う.
定式化
基礎方程式は2次元非圧縮性流体の渦度方程式 \begin{align} % \frac{\partial \omega}{\partial t} + J(\omega, \psi) &= \frac{1}{\mathrm{Re}}\nabla^2\omega \label{VorticityEq} % \end{align} と,渦度 $\omega(x,y,t)$ と流れ関数 $\psi(x,y,t)$ に関するポアソン方程式(Poisson equation) \begin{align} % \nabla^2 \psi &= - \omega % \end{align} である. ここで$J(\cdot, \cdot)$はヤコビアン(Jacobian)で, $J(f,g) := \frac{\partial ( f, g )}{\partial ( x, y )} = \frac{\partial f}{\partial x}\frac{\partial g}{\partial y} - \frac{\partial f}{\partial y}\frac{\partial g}{\partial x}$, $\nabla^2$は2次元ラプラシアン(Laplacian)で, $\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$である. $\mathrm{Re}$はレイノルズ数で,平面ポアズイユ流の$x$方向の最大速度 $U$ と分子粘性係数 $\nu$,そして管路の幅$2L$を用いて, \begin{gather} \mathrm{Re} := \frac{UL}{\nu} \end{gather} と定義する. ここで, 速度ベクトル $\boldsymbol{u}= u \boldsymbol{i} + v\boldsymbol{j}$ と流れ関数の間には \begin{align} % u = \frac{\partial \psi}{\partial y}, &\quad v = - \frac{\partial \psi}{\partial x} % \end{align} の関係があることを注意しておく.
境界条件として,$y$ 方向には $y=\pm 1$ で $u=0$,$v=0$ を課す.これは壁を $y=\pm 1$ に置いたことに対応する. $x$ 方向には周期境界条件を課す.
撹乱を加えたときの流れの安定性を調べたいので,撹乱についての方程式を導出する. 平面ポアズイユ流を基本流 $\overline{u}(y)$ として,撹乱を $u'(x,y,t):= u(x,y,t) - \overline{u}(y)$ とする. 撹乱の支配方程式は, \begin{align} % \frac{\partial \omega'}{\partial t} + J(\omega', \overline{\psi}) + J(\overline{\omega}, \psi') + J(\omega', \psi') &= \frac{1}{\mathrm{Re}}\nabla^2\omega' \label{PerturbedVorticityEq} % \end{align} \begin{align} % \nabla^2 \psi' &= - \omega' % \end{align} となる. また,撹乱として $x$ 方向の波数 $\alpha$、複素位相速度 $c$ の波型撹乱を考える.すなわち, $u'(x, y, t) := \hat{u}(y)\exp \left[ i\alpha ( x - ct ) \right]$ を考える.撹乱の振幅が微小であり,撹乱の二次の項を無視できるとすれば, \begin{align} % i\alpha( \overline{u} - c ) ( \partial_y^2 -\alpha^2 ) \hat{\psi} - i\alpha \overline{u}_{yy} \hat{\psi} - \frac{1}{\mathrm{Re}}( \partial_y^2 -\alpha^2 )^2 \hat{\psi} &= 0 % \end{align} となる.これを \begin{align} \hat{\psi}(\pm 1) = 0, &\qquad \hat{\psi}'(\pm 1) = 0 \end{align} の境界条件の下で解く. 前者は撹乱により流量が変化しないこと,後者は壁ですべりなし条件を満たすことに対応する.
離散化
渦度と流れ関数を チェビシェフ(Chebyshev)多項式を用いた基底関数で展開し,その展開係数に関する 一般化固有値問題を構成する.
具体的には,展開係数の $N+1$ 個の方程式からなる連立一次方程式が,ガウス・ロバット点(Gauss-Lobatto points)に おいて成り立つことを要請する(コロケーション法). ガウス・ロバット点は $N+2$ 次のチェビシェフ多項式が極値を取る点 \begin{align} % y_m = \cos\left( \frac{m\pi}{N+2} \right), \qquad (m=1,2,\dots,N+1) % \end{align} のことである.
つまり,流れ関数の撹乱 $\hat{\psi}$ を \begin{align} % \hat{\psi}(y) = \sum_{n=0}^{N} a_n F_n(y) % \end{align} と展開する.ここで $F_n(y)$ を$n$番目のの基底関数,$a_n$ をその係数とした. 基底関数に要請されるのは,壁で境界条件を満たすこと,である. このとき, $F_n(y)$ を, \begin{align} F_n(y) = (1-y^2)^2 T_n(y) \end{align} と置く. この基底関数は Heinrichs' basis と呼ばれ,連立一次方程式の係数行列の 条件数(condition number)を小さくすることができる (Boyd, 2001, p.144; 条件数については,コラム: 条件数についてを参照のこと).
この展開係数 $a_n$ を縦に並べた列ベクトルを $\mathbf{x}$ とすると, \begin{align} % A\mathbf{x} = cB\mathbf{x} % \end{align} という形の一般化固有値問題に帰着される.
プログラム
レイノルズ数 $\mathrm{Re}$ と波数 $\alpha$ を与えると第一不安定モード/最小減衰モードの成長率 (以下,単に成長率と呼ぶ)と それに対応するモード(固有関数)を出力するプログラムコードを 示す(poisg_lapack.f90).
ここで,非対称行列の一般化固有値問題を解くために Lapack の zgegv サブルーチン を用いた.
プログラムコードを少し変更し $\mathrm{Re}$ と $\alpha$ について繰り返し成長率を求めるように 変更したものを示す(poisg_lapack2.f90). これを用いれば,グラフプロットツール(gnuplot)を用いることで, 成長率がゼロとなる「中立曲線」を求めることができる.
プログラムと描画スクリプト一覧
結果
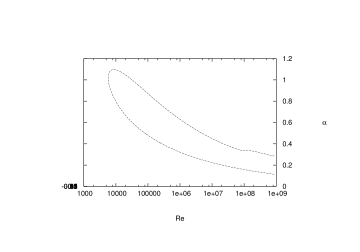
線形不安定の中立曲線(点線)を $\mathrm{Re}$-$\alpha$ 平面にプロットしたものを示す. 中立曲線の外側が線形安定領域,内側が線形不安定領域である. この図から,$Re \approx 5800$ で $\alpha \approx 1$ の撹乱が もっとも低いレイノルズ数で線形不安定となることが分かる. また,高レイノルズ数ではむしろ $\alpha \approx 1$ の撹乱は安定であり, より波数 $\alpha$ の小さい撹乱が線形不安定であることが分かる.
図は gnuplot で ps ファイルを出力した上で,さらに ImageMagick の convert コマンドを用いて, convert -rotate 90 -scale 50% -density 144 poisg_lapack2.ps growth.png として png ファイルを生成した.
付録:チェビシェフ多項式とチェビシェフの微分方程式
チェビシェフ多項式は特殊関数の一種で, \begin{align} T_n(y) &:= cos n\theta, \quad y = cos\theta \end{align} と定義される. チェビシェフの微分方程式 \begin{align} (1-y^2) T_n'' - yT_n' + n^2T_n = 0 \end{align} の解であり, 昇降関係式として \begin{gather} T_{n+1}(y) - 2yT_n(y) + T_{n-1}(y) = 0, \\ T_{n \pm 1}(y) = \left( y \mp \frac{(1-y^2)}{n} \frac{d}{dy} \right) T_n(y) \end{gather} が成り立つ.
コラム:条件数について
行列の条件数とは,正規行列について言えば,行列の最大固有値と最小固有値の大きさの比である. 数値計算で行列を取り扱う際には,行列の条件数は小さい方が都合が良い. 数値計算では実数は浮動小数点数として扱われるため,有限の桁数の数を取り扱うことになるが, 条件数が大きすぎると,その桁数を越えてしまい,誤差の原因となるからである. 従って,定式化の段階で取り扱う行列の条件数を減らすか, 計算過程で用いる浮動小数点数の精度を, 通常よく用いられる倍精度よりも高精度のもの(倍々精度や四倍精度など)に 変更するなどの工夫が必要になる. 条件数が大きいとき、その行列は悪条件(ill-conditioned)であると言う。
ノート
本ページの内容は,水島二郎,藤村薫 (2003) を大いに参考にした. また,プログラムコードは FORTRAN 77 版を水島教授から提供して頂き, それを筆者が Fortran 90 版に書き直した.
参考文献
- 水島二郎,藤村薫,2003: 流れの安定性,朝倉書店,240 pp.
- Boyd, J. P., 2001: Chebyshev and Fourier Spectral Methods, 2nd Edition, Dover, New York, 688 pp.